Using the Runge-Kutta 2nd order
Ralston method with a step size of 5 seconds, the distance in meters traveled by
the body from t=2 to
t=12 seconds
is estimated most nearly is
3904.9
3939.7
6556.3
39397
Q5. The Runge-Kutta 2nd order method
can be derived by using the first three terms of the Taylor series of
writing the value of yi+1 (that
is the value of y at
xi+1 )
in terms of yi (that
is the value of y at
xi)
and all the derivatives of y at
xi .
If h=xi+1-xi,
the explicit expression for yi+1 if
the first three terms of the Taylor series are chosen for solving the
ordinary differential equation
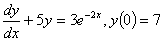
would be
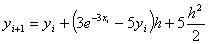
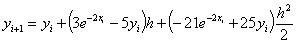
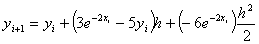
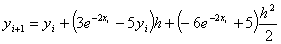
Q6. A spherical ball is taken out of a furnace
at 1200K and is allowed to cool in air. Given the following,
radius of ball = 2 cm
specific heat of ball = 420
J/(kg-K)
density of ball = 7800
convection coefficient = 350
J/s-m^2-K
The ordinary differential equation is
given for the temperature,
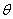 of the ball
of the ball
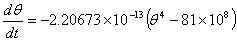
if only radiation is accounted for. The
ordinary differential equation if convection is accounted for in
addition to radiation is
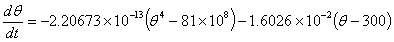
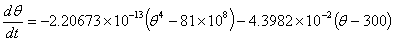
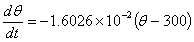
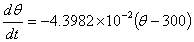
Complete Solution
Multiple choice questions on other topics