|
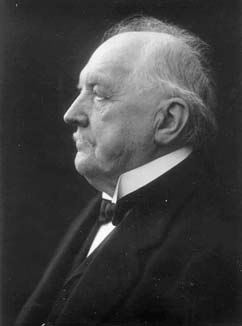 Martin Wilhelm Kutta was born on the 3rd
of November 1867 in Pitschen, Upper Silesea (the former border
to Russian Poland, which is now Byczyna, Poland)
and died on the 25th of
December 1944 in Fürstenfeldbruck,
Germany. He had one older brother, Karl, and both their mother,
Anna Koschinsky, and father, Wilhelm Kutta, died when they were
young children. As a result, the brothers left their home to
live with their uncle in Breslau (still in Poland), where they
attended the Gymnasium. A gymnasium is a selective school
similar to a middle school or junior high school found in the US
for pupils ranging from 13 to 16 years of age. The gymnasium is
offered to academically promising students and prepares them for
entry into a university for advanced academic study. Following
graduation from the Gymnasium, Kutta was educated at the
University of Breslau, namely in mathematics, from 1885 to
1890. After that, he traveled to Munich where he attended
university from 1891 to 1894.
Mathematics was always
Kutta’s primary subject, but he had broad interests and explored
these through courses in languages, music, literature, history,
and art throughout his studies. Because of his thirst for
knowledge and love of learning, he studied and explored these
interests and applied his found knowledge throughout his life.
As such, he acquired a comprehensive and thorough knowledge of
several subjects. He was indeed an extremely intellectual,
driven, and knowledgeable individual whom many respected and
acknowledged.
While attending the
Technische Hochschule (Institute of Technology) in Munich, Kutta
was appointed as an assistant in mathematics and physics. In
1894, he became an assistant to Walther Franz Anton von Dyck,
conducting the exercise classes for von Dyck’s course on higher
mathematics. During the year spanning 1898 to 1899, Kutta left
Munich to study in England at the University of Cambridge. In
1900, Kutta was awarded his doctorate from the Technische
Hochschule of Munich. His thesis title was “Beiträge zur
näherungsweisen Integration totaler Differentialgleichungen”
(“Contributions for the Approximate Integration of Total
Differential Equations”). His thesis paper was published
in 1901 and contains the now famous Runge-Kutta methodology for
solving ordinary differential equations. Kutta had two advisors
who oversaw his studies and research in Munich. They were Carl
Louis Ferdinand von Lindemann and Gustav A. Bauer.
Interestingly, Lindemann (1852-1939) was the German
mathematician who proved, with his publication in 1882, that
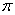 (pi)
is a transcendental number. (Meaning (pi)
is a transcendental number. (Meaning
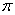 is
not a root of any polynomial with rational coefficients.) is
not a root of any polynomial with rational coefficients.)
After acquiring his
doctoral degree, Kutta worked as a professor at Technische
Hochschule in Munich. Interestingly, Kutta never took the
qualifying examinations required to teach in Bavarian secondary
schools because he preferred to teach (and assist in teaching)
in university.
A fellow teacher at
Technische Hochschule in Munich, Sebastian Finsterwalder, was
extremely interested in aviation. As such, he brought Kutta
several photographs of early aircraft. Being foremost a
mathematician, Kutta became fascinated by aerodynamics, the
mathematics that make aviation possible. This great interest and
his keen intellect lead Kutta to discover the formulas used to
relate the lift on an aerofoil to the fluid circulation around
it. In 1902, Kutta submitted his habilitation thesis on
aerodynamics to the Technische Hochschule at Munich. (A
habilitation is the highest academic qualification a scholar can
achieve. It is obtained after receiving a research doctorate
(PhD) and requires the candidate to write a professorial thesis
based on independent scholarship, i.e. without supervision or
guidance by institutional faculty. As such, the level of writing
must be much higher than that of a research doctoral in terms of
content quality and quantity.) The main theorem in this
habilitation was the
Zhukovsky-Kutta theorem, which derives the lift equation on an
aerofoil. Kutta made later contributions to aerodynamics with
his publications through the Königlich Bayerischen Akademie der
Wissenschaften of Munich (Royal Bavarian Academy of Sciences) in
1910 and 1911. One in particular was entitled “Über ebene
Zirkulationsströmungen nebst flugtechnischen Anwendungen” (“Over
Smooth Circulation Flows Together with Aeronautical
Applications”) and contains his mapping theorem from function
theory.
In 1907, Kutta
was promoted to extraordinary professor in Applied Mathematics.
In 1909, he moved to the University of Jena and in 1910 he was
appointed as a professor at the University of Aachen. Finally in
1911, he became a professor at the Technische Hochschule in
Stuttgart and stayed there until he retired from teaching in
1935. During his stay at Stuttgart, Kutta concentrated on
teaching engineering students who could greatly benefit from his
inspiring lectures and vast knowledge.
Two other interesting
research topics Kutta explored in his scholarly endeavors were
on glaciers and the history of mathematics. Sebastian
Finsterwalder, as before with aviation, spurred Kutta’s interest
in glaciers. As a result, Kutta made measurements based off of
photographs of the East Alps and worked with others to construct
maps of areas covered by glaciers. Eventually, he published his
work on glaciers entitled “The Gepatschferner in AD 1896.” As
for the history of mathematics, Kutta was strongly interested in
history (namely historical literature), attended seminars on the
history of mathematics, and even wrote a paper on Wallis’s 1659
work on integration and the length of an ellipse. In addition,
after attending seminars at the
Technische Hochschule of Munich on the
history of mathematics, Kutta wrote several essays on the
history of geometry and mathematics principles.
Bibliography
Venn, J.; Venn, J. A., eds. (1922–1958). "Kutta, Wilhelm
Martin”. Alumni Cantabrigienses (10 vols) (online ed.).
Cambridge University Press. Retrieved November 20, 2012.
O’Connor, John
J; Robertson, Edmund F. “Martin Wilhelm Kutta”. August 2006.
MacTutor History of Mathematics archive, University of St.
Andrews, Scotland. Retrieved November 20, 2012. http://www-history.mcs.st-andrews.ac.uk/Biographies/Kutta.html.
Bulirsch, R; Breitner, M. “Wilhelm Martin Kutta 1867-1944”.
Technische Universität München, Fakultät für
Mathematik. Retrieved November 20, 2012.
http://www-hm.ma.tum.de/geschichte/node21.html
Butcher, J.C.;
Wanner, G. “Runge-Kutta Methods: Some Historical Notes”.
ELSEVIER: Applied Numerical Mathematics 22 (1996) 113-151
(online book). Retrieved November 25, 2012.
Home >
Biographies
|