|
Pick the
most appropriate answer.
Q1.
The Newton-Raphson
method of finding roots of nonlinear equations falls under the category
of _______ methods.
bracketing
open
random
graphical
Q2. The Newton-Raphson method formula for finding the square root of a real
number R from the equation
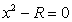 is, is,
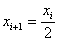
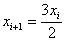
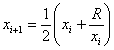
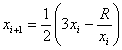
Q3. The next iterative value of the root of
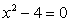 using Newton-Raphson method, if the initial guess is 3, is
using Newton-Raphson method, if the initial guess is 3, is
1.500
2.066
2.167
3.000
Q4. The
root of the equation f(x)=0 is found by using
the Newton-Raphson
method. The initial
estimate of the root is
x0=3,
and f(3)=5. The angle the line tangent to the function f(x)
makes at x=3 with the x-axis is 570. The next estimate of the root,
x1
most nearly is
-3.247
-0.2470
3.247
6.247
Q5. The root of
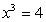 is found by using
the Newton-Raphson method.
The successive iterative values of the root are given in the
table below is found by using
the Newton-Raphson method.
The successive iterative values of the root are given in the
table below
|
Iteration
Number
|
Value
of Root
|
|
0
|
2.0000
|
|
1
|
1.6667
|
|
2
|
1.5911
|
|
3
|
1.5874
|
|
4
|
1.5874
|
The iteration number at which I would
first trust at least two significant digits in the answer is
1
2
3
4
Q6.
The ideal gas law is given by
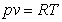
where where p is the pressure, v is the specific volume, R is the
universal gas constant, and T is the absolute temperature.
This equation is only accurate for a limited range of pressure and
temperature. Vander Waals came up with an equation that was accurate for
larger ranges of pressure and temperature given by
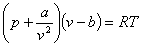
where a and b are
empirical constants dependent on a particular gas. Given the value of
R=0.08, a=3.592, b=0.04267, p=10 and T=300 (assume all units are consistent), one is
going to find the specific volume, v, for the above values. Without
finding the solution from the Vander Waals equation, what would be a good
initial guess for v?
0
1.2
2.4
4.8
Complete Solution
Multiple choice questions on other topics
|
