|
|
|
|
|
|
Pick the most
appropriate answer.
|
Q1. The LU decomposition method is computationally more efficient than Naïve
Gauss elimination method for solving
a
single set of simultaneous linear equations
multiple
sets of simultaneous linear equations with different coefficient
matrices and the same right hand side vectors.
multiple
sets of simultaneous linear equations with the same coefficient matrix but different right hand sides.
less
than ten simultaneous linear equations.
Q2.
The lower triangular matrix [L] in the [L][U]
decomposition of the matrix given below
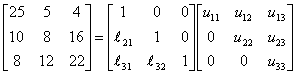 is is

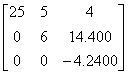

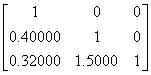
Q3.
The upper triangular matrix [U] in
the [L][U] decomposition of the matrix given below
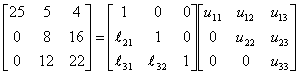 is is

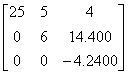

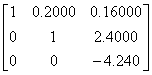
Q4.
For a
given 2000 2000
matrix [A], assume that it takes about 15 seconds to find the inverse of
[A] by use of the [L][U] decomposition method, that is, finding the [L][U]
once, and then doing forward substitution and back substitution 2000
times using the 2000 columns of the identity matrix as the right hand
side vector. The approximate time, in seconds, that it will take to
find the inverse if found by repeated use of the Naive Gauss elimination
method, that is, doing forward elimination and back substitution 2000
times by using the 2000 columns of the identity matrix as the right hand
side vector is most nearly 2000
matrix [A], assume that it takes about 15 seconds to find the inverse of
[A] by use of the [L][U] decomposition method, that is, finding the [L][U]
once, and then doing forward substitution and back substitution 2000
times using the 2000 columns of the identity matrix as the right hand
side vector. The approximate time, in seconds, that it will take to
find the inverse if found by repeated use of the Naive Gauss elimination
method, that is, doing forward elimination and back substitution 2000
times by using the 2000 columns of the identity matrix as the right hand
side vector is most nearly
300
1500
7500
30000
Q5. The algorithm for solving the
set of n equations [A][X] = [C],
where [A] = [L][U] involves solving
[L][Z] = [C] by forward substitution.
The algorithm to solve [L][Z]=[C] is given by
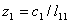
for i from 2 to n do
sum = 0
for j from 1 to
i do
sum = sum +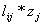
end do
zi
= (ci – sum) / lii
end do
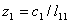
for i from 2 to n do
sum = 0
for j from 1 to
(i-1) do
sum = sum +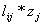
end do
zi
= (ci – sum) / lii
end do
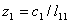
for i from 2 to n do
for j from 1 to
(i-1) do
sum = sum +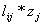
end do
zi
= (ci – sum) / lii
end do
for i from 2 to n do
sum = 0
for j from 1 to
(i-1) do
sum = sum +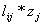
end do
zi
= (ci – sum) / lii
end do
Q6. To solve boundary value problems,
the finite
difference methods are used resulting in simultaneous linear equations
with tridiagonal coefficient matrices. These are solved using the specialized [L][U] decomposition method.
The set of equations in matrix form with a tridiagonal coefficient
matrix for
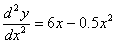 , ,
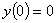 , ,
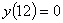 , ,
using the finite difference method with a
second order accurate central divided difference method and a step size
of 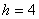 is is

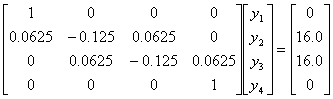


Complete Solution
Multiple
choice questions on other topics
| 