|
|
|
|
|
|
Pick the most
appropriate answer.
|
Q1.
Given
(x1,y1), (x2,y2),
..., (xn,yn) best
fitting data to y=f(x) by
least squares requires minimization of
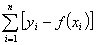
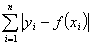
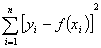
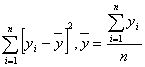
Q2.
The following data
|
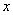 |
1 |
20 |
30 |
40 |
|
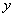 |
1 |
400 |
800 |
1300 |
is regressed with least squares regression
to y=a0+a1x.
The value of a1 most
nearly is
27.480
28.956
32.625
40.000
Q3.
The
following data
|
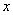 |
1 |
20 |
30 |
40 |
|
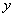 |
1 |
400 |
800 |
1300 |
is regressed with least squares regression
to y=a1x.
The value of y=a1x most
nearly is
27.480
28.956
32.625
40.000
Q4.
An
instructor gives the same
y vs x data
as given below to four students and asks them to regress the data with
least squares regression to
y=a0+a1x.
|
|
1 |
10 |
20 |
30 |
40 |
|
|
1 |
100 |
400 |
600 |
1200 |
Each student comes up with four different
answers for the straight line regression model. Only one is correct.
The correct model is
y=60x-1200
y=30x-200
y=-139.43+29.684x
y=1+22.782x
Q5. A
torsion spring of a mousetrap is twisted through an angle of 1800.
The torque vs angle data is given below.
|
Torsion, T,
N-m |
0.110 |
0.189 |
0.230 |
0.250 |
|
Angle,
θ, rad |
0.10 |
0.50 |
1.1 |
1.5 |
The
amount of strain energy stored in the mousetrap spring in Joules is
0.29872
0.41740
0.84208
1561.8
Q6.
A
scientist finds that regressing the y
vs x data
given below to
y=a0+a1x results
in the coefficient of determination for the straight-line model,r2 being zero.
|
x |
1 |
3 |
11 |
17 |
|
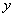 |
2 |
6 |
22 |
? |
The missing value for y at x=17
most nearly is
-2.4444
2.0000
6.8889
34.000
Complete Solution
Multiple
choice questions on other topics
|
