|
Q1.
Which of the
following statements is incorrect?
Direct search methods are useful when the
optimization function is not differentiable
The gradient of
f(x,y)
is the a vector pointing in the direction of the steepest slope at that
point.
The Hessian is the Jacobian Matrix of
second-order partial derivatives of a function.
The second derivative of the
optimization function is used to determine if we have reached an optimal
point.
Q2. An
initial estimate of an optimal solution is given to be used in
conjunction with the steepest ascent method to determine the maximum of
the function. Which of the following statements is correct?
The
function to be optimized must be differentiable.
If the initial estimate is different
than the optimal solution, then the magnitude of the gradient is
nonzero.
As more iterations are performed, the
function values of the solutions at the end of each subsequent iteration
must be increasing.
All 3 statements are correct.
Q3.
What are the gradient and the determinant of the Hessian of the function
f(x,y)=x2y2 at its global optimum?
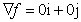 and and
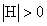
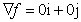 and and
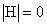
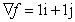 and and
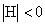
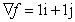 and and
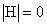
Q4.
Determine the gradient of the function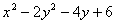 at
point (0, 0)? at
point (0, 0)?
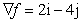
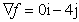
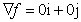
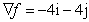
Q5.
Determine the determinant of hessian
of the function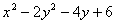 at
point (0, 0)? at
point (0, 0)?
2
-4
0
-8
Q6.
Determine the minimum of the function
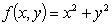 ?
Use the point (2, 1) as the initial estimate of the optimal solution.
Conduct one iteration. ?
Use the point (2, 1) as the initial estimate of the optimal solution.
Conduct one iteration.
(2,1)
(-6,-3)
(0,0)
(1,-1)
Complete Solution
Multiple choice questions on other topics
|
