|
Q1. Which of the following
statements is incorrect regarding the Equal Interval Search and
Golden Section Search methods?
Both
methods require an initial boundary region to start the search
The
number of iterations in both methods are affected by the size of
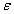
Everything else being equal, the Golden Section Search method should
find an optimal solution faster.
Everything else being equal, the Equal Interval Search method should
find an optimal solution faster.
Q2. Which of the following parameters is not required to use the
Golden Section Search method for optimization?
The
lower bound for the search region
The
upper bound for the search region
The
golden ratio
The
function to be optimized
Q3. When
applying the Golden Section Search method to a function
f(x) to
find its maximum, the
f(x1)>f(x2)
condition
holds true for the intermediate points
x1
and
x2.
Which of the following statements is incorrect?
The new
search region is determined by
[x2, xu
]
The
intermediate point
x1 stays as one of the intermediate
points
The upper
bound xu stays
the same
The new
search region is determined by [xl,
x1 ]
Q4.
In the graph
below, the lower and upper boundary of the search is given by
x1 and
x3
respectively. If x4 and
x2 are
the initial intermediary points, which of the following statement is
false?
The
distance between x2 and
x1 is
equal to the distance between x4 andx3
The
distance between x4 and
x2
is
approximately 0.618 times the distance between
x2 and
x1
The distance between
x4 and
x1 is
approximately 0.618 times the distance between
x4 and
x3
The distance between
x4 and
x1 is equal to the distance between
x2 andx3
Q5.
Using the Golden Section Search
method, find two numbers whose sum is 90 and their product is as large
as possible. Use the interval [0,90].
30 and 60
45 and 45
38 and 52
20 and 70
Q6.
Consider the problem of finding the minimum of the function shown below.
Given the intermediate points in the drawing, what would be the search
region in the next iteration?
[x2,
xu ]
[x1,
xu ]
[xl,
x1 ]
[xl,
x2 ]
Complete Solution
Multiple choice questions on other topics
|
